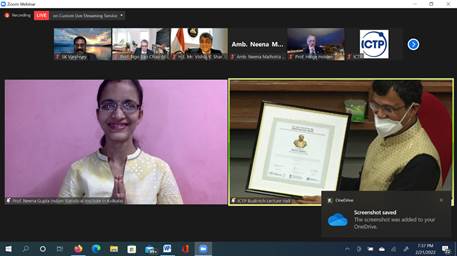
The Ramanujan Prize for Young Mathematicians was awarded to Professor Neena Gupta, a mathematician of the Indian Statistical Institute in Kolkata, in a virtual ceremony on 22^nd February 2022. She received the award for the year 2021 for her outstanding work in affine algebraic geometry and commutative algebra.

 

On the behalf of Secretary and Department, Shri Sanjeev Varshney, Head, International Cooperation Division, DST, congratulated Dr. Neena Gupta and said that the award conferred to a female researcher will encourage other female researchers all around the world to take up mathematics as their career. “I am also sure that this recognition will motivate her further to expand research with more noteworthy outcomes in the future. It will also inspire the researchers and young mathematicians not only in our country but in the entire developing world, to undertake research in mathematical sciences,” he added.

 

The prize is awarded annually to a researcher from a developing country funded by the Department of Science and Technology (DST) of the Government of India in association with ICTP (International Centre for Theoretical Physics) and the International Mathematical Union (IMU).

 

It is given to young mathematicians less than 45 years of age who have conducted outstanding research in a developing country. It is supported by DST in the memory of Srinivasa Ramanujan, a genius in pure mathematics who was essentially self-taught and made spectacular contributions to elliptic functions, continued fractions, infinite series, and analytical theory of numbers.

 

Professor Gupta's solution for solving the Zariski cancellation problem, a fundamental problem in Algebraic Geometry, earned her the 2014 Young Scientists Award of the Indian National Science Academy (NSA). The NSA described her solution as ‘one of the best works in algebraic geometry in recent years done anywhere’. The problem was posed by one of the most eminent founders of modern Algebraic Geometry, Oscar Zariski, in 1949. In an interview with an American university, Gupta describes the problem as ---The cancellation problem asks that if you have cylinders over two geometric structures, and that have similar forms, can one conclude that the original base structures have similar forms?

 

 

 

 

*****

SNC / RR

(Release ID: 1800354) Visitor Counter : 6305